I was invited recently to give a talk to Reach Out and Read Minnesota, a lovely organization that supports early literacy development by connecting with children and caregivers in medical offices. They are beginning to explore similar work for early math development. This talk was part of that effort.
I had three messages for them, which I will pass along to you, along with the relevant slides for each message.
Children know and can do more math than their caregivers expect
Children know and can do more math than their parents and teachers think they can. An example is this study of young children’s knowledge of place value.
You can see society’s low expectations for children’s mathematical competence in the materials we generally provide for early math. For example, here is a T-shirt currently for sale at the Gap.

We think children’s geometry learning is limited to names for shapes, and so we show one example of each shape—always the canonical one, and rarely offer variants or relationships between them. A hexagon is always regular (i.e. same measure for each side; same measure for each angle), and always oriented with a horizontal base.
Shapes books have one kind of shape per page, and rarely introduce special cases. There are always separate pages for squares and for rectangles.
As a culture, we understand that children can interact with complex narratives in picture books and film. We know that they can empathize with more than one character in a story; even when those characters are in conflict. But we don’t understand that children can handle mathematical complexity of any kind—not even a straightforward proposition such as squares are special rectangles.
Look at that T-shirt again. The square and the rectangle aren’t even next to each other, or the same color, or anything that might suggest a relationship. They’re two different shapes, just as the pentagon and oval are different shapes.
There are other possible ways to do this work, but it requires a shift in expectations. If we expect that children will notice and play with complex mathematical relationships, we’ll design richer and more nuanced things for their environment.
Consider how much fun this young one is having with a set of shapes puzzles and a bubble on a warm summer’s day.

That Z-shaped hexagon in the lower-right-hand corner of the photograph is asymmetrical, so it won’t fit if you flip it upside down. You can’t just rotate the shape on the table to make it fit; you need to decide which is the top and which is the bottom. Most shapes puzzles have little handles on the pieces—or have pictures on top and are blank on the bottom. The puzzle does that thinking for you. This puzzle does not because asymmetry is a thing children can figure out for themselves.
In the exhibit below, I contrast the T-shirt with toys we have at Math On-A-Stick. One hexagon on the left. Nine variations on hexagons on the right. One “oval” on the left; eight “ellipses” on the right. (For the record, I am not opposed to the term “oval,” but why can’t we also use “ellipse”? If children can handle “Tyrannosaurus rex” then surely they can handle “ellipse,” right?)

These things don’t exist in every child’s life because of the adults in their life, not because the children reject these things.
Quick story: A young child—probably two-ish—at Math On-A-Stick was playing with the ellipses puzzle one morning, and the child’s mother noticed the word “Ellipses” at the top of the puzzle after a few minutes of play. She shifted her language and began asking which “ellipse” the child wanted to do next.
This brings me to the next message…
Young children learn math like they do language
Children are logical creatures; more logical than you probably expect or notice. Most of their learning is cultural, though. That is to say, children learn language from repeated exposure, not from dictionaries. If you want children with large vocabularies, you’ll need to use lots of different words around them. If you want children who read, you’ll need to read with them and to be seen reading by them. We understand this in American culture, and we have robust messaging around it.
It’s the same for math.
Children learn about multidigit numbers through the experiences they have in their lives. Addresses, bus routes, prices, and more—all contribute to children’s understanding that, say, 345 is greater than 78.
We can support children’s math learning by giving them more opportunities to play with math objects. The puzzles from earlier on are one version of this, and the countdown blocks and magnetic hundreds chart below are additional examples.
In a study of the Bedtime Math app, researchers concluded that in math anxious households there is almost no math talk. Math—like death, religion, and sexuality—is a topic that often makes lots of adults anxious, and causes them to change the subject. In that same study, they found that infusing even small amounts of math talk into such a household has a positive impact on children’s math learning. A little bit of low-stakes math talk opens the door to more of it, which leads to more learning.
Given an opportunity, children will pursue sophisticated math ideas
We see this day in and day out at Math On-A-Stick.
In the image below, the object on the left provides fewer opportunities for sophisticated ideas than the object on the right. That is because the Multiplication Machine is designed to do exactly one thing—act as a set of organized, mechanical flash cards. Each of the 81 buttons shows two numbers multiplied on top, and then their product on the front when the button is popped up. There is social pressure (from parents, other children, etc.) to do the thing you are supposed to do—recite multiplication facts and check your answers one at a time)—instead of the thing you really want to do—make patterns, draw pictures, invent games.
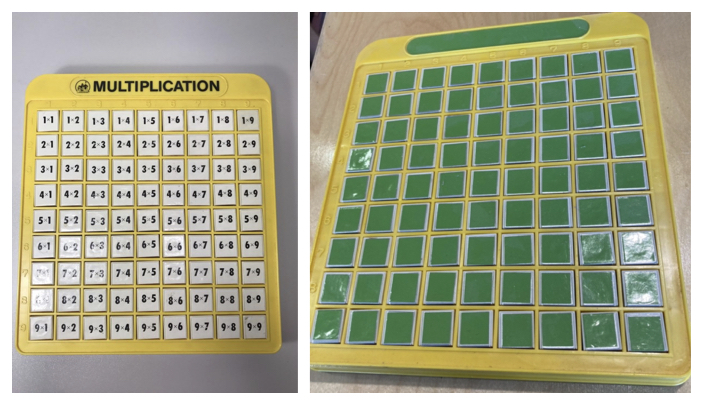
We cover all those numbers with precision-cut sign vinyl to convert these into Pattern Machines, and we offer up a couple dozen to the children at Math On-A-Stick. Those children play with Pattern Machines in ways you’re not supposed to play with Multiplication Machines, and along the way, they do more mathematics. They make patterns and paths. They count and strategize. The child in these next images has posed for herself a problem in combinatorics: How many ways can you make enclosed dog pens on a 9 by 9 Pattern Machine? You can see several ways she has found on the machines going off into the distance.

These three messages intertwine. If you provide opportunities for sophisticated ideas, you’ll have more to talk about. Having more to talk about extends the conversation and children’s exposure to mathematical ideas; but those conversations are really only possible if we accept that children have the potential to think and act in sophisticated ways mathematically.
Interested in talking more about ways to support children’s math learning? Need help designing a thing or experience for math learning? Want me to talk to your organization as I did with Reach Out and Read Minnesota or in the media as I did with Minnesota Public Radio or KQED’s MindShift? Get in touch!


