I had an opportunity to play math with children and parents at a local elementary school last night. (Shoutout to Oak Ridge Elementary! Thanks for hosting!) The Pattern Machines were a big hit.
One seven-year old spent some time deciding what to make and a couple of minutes idly punching buttons before she got down to work. In a short time, she declared she had made a square and presented it for my approval.

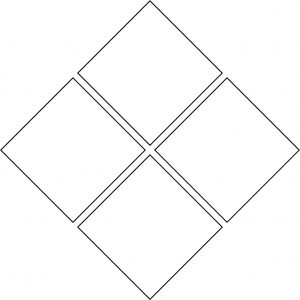
I noticed her square, as this seemed important to her, and I told her it gave me an idea. On my own Pattern Machine (leaving hers untouched—an important tenet of this work is never to take the pencil out of the child’s hand!), I made the thing below and asked her whether I too had made a square.

“No. That’s a diamond,” she declared.
I rotated my Pattern Machine 45°.

“Now?” I asked.
“Now it’s a square.” she said with a knowing look.
Diamond also came up when I talked with children and adults about a page in Which One Doesn’t Belong?

I used to think that diamond was a lazy term for rhombus, but it is not. Diamond has a stable and robust meaning that is different from rhombus. On that Which One Doesn’t Belong? page, the upper right and the lower left shapes are diamonds. The lower right is not, yet each of these three is a rhombus.
Also sometimes a pentagon is a diamond.
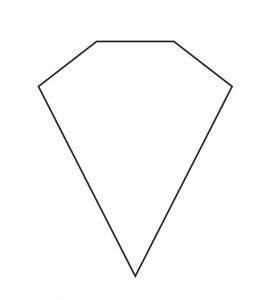
So I propose we treat diamonds as we do other mathematical objects.
Let’s build rock solid definitions of them—definitions that we can take as shared and use to sort diamonds from not-diamonds.
Let’s investigate the consequences of those definitions.
Let’s investigate conjectures and prove theorems.
Together, let’s build a rich field of mathematical inquiry.
I’ll start us off. Some diamonds can be cut into smaller diamonds, as in the example below. Can ALL diamonds be cut into smaller diamonds? If not, which ones can and which ones cannot?