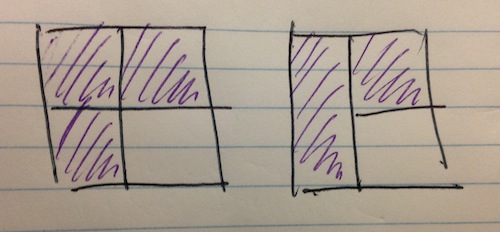A propos of nothing one day, I ask Griffin (9 years old at the time, finishing up fourth grade) a question.
Me: Griff, imagine you are baking cookies and you need
cup of sugar, but you only have a
cup measure. How would you get
cup?
He thinks about this for a moment.
Griffin (9 years old): You put
cup of whatever you’re measuring.
Me: Sugar.
G: Does it matter?
Me: No. I suppose not.
The conversation could end here and I would be delighted. But it does not end here.
G: You put that into the bowl, then you fill the cup halfway and put that in.
Me: And that’s
cup?
G: Yes.
Me: How do you know?
G: Because
is a half, and then half of a half.
Me: Yeah. That is what you just described. How do you know that that’s right?
G: Like a square. If you shade in half of it, and then half of what’s left, that’s the same as shading
of it.
So What Do We Learn?
One question division helps answer is how many of this are in that? My question of Griffin asked how many halves are in three-fourths? This is a division question.
Griffin may not know that it is a division question. That is fine. He is thinking about a specific example of how many of this are in that? This will lead to good things further down the line.
That he sees “sugar” as a non-essential detail of the story is lovely. This will serve him well.
Griffin’s mental image for this task is a common one. He can see three fourths of a square in his mind, and he can see that this is the same as one-and-a-half halves of a square.
Finally, we learn (because I am about to tell you) that this scenario could never really happen when baking in our home. I have an awesome set of measuring cups (pictured below): ,
,
,
,
, 1 and
. (A friend—and friend of the project—has pledged to donate her
cup measure to the Talking Math with Your Kids cause.)
Starting the Conversation
There are so many ways to raise the question how many of this are in that? Measure each other in inches, wonder how many feet tall that is. Count your quarters, wonder how many dollars that is. Repeat with nickels, or dimes. Bake a batch of cookies using only the cup measure.
And you can read through previous division posts for more ideas.