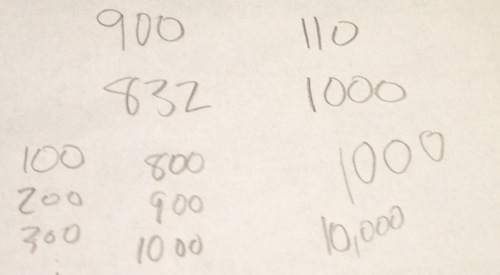There was a while when Tabitha (five and six years old at the time) would try to get away without wearing underpants when she dressed herself. Those days are pretty much over, but I still like to make sure she has done the complete job, so I ask her from time to time.
Tabitha (7 years old): I’m dressed!
Me: Are you wearing underpants?
T: Yup—Dora the Explorer.
Don’t worry. The child is not wearing these in the picture.
Me: Nice. How do you feel about your Dora the Explorer underpants?
T: I don’t really like Dora that much, but I have a thousand of them.
Me: That’s a lot.
T: I counted them once.
Me: All one thousand?
T: No. I don’t really have a thousand. I don’t even know how to count to a thousand. Just to ten hundred.
I pause for a moment. Does she mean one-hundred-ten? Can’t be. She must know that one-hundred-eleven comes next.
Me: Ten hundred. You mean like after nine hundred is ten hundred?
T: Yeah. That’s as high as I know how to count. I don’t even know how many a thousand is.
Me: A thousand is ten hundred.
T: Oh. Cool.
A few minutes later, I get an idea. I wonder how she would write ten hundred. She needs to get out the door for school so I make it quick. I ask her to read some numbers out loud as I write them.
- 900
- 832
- 110
- 1000.
For that last one, she says one thousand.
I ask how she would write ten hundred.
She writes, “1000”.
T: It’s the same.
Me: Because I just told you that. Right. How would you have written ten hundred before I told you it was the same as one thousand?
She shrugs her shoulders. Drat. Moment lost. We talk about hundreds for a moment. One hundred, two hundred, etc. up to ten hundred.
Then I have one more.
Me: OK. Last one, then off to school. How would you read this one?
I write 10,000.
She looks for a moment. And thinks.
T: Ten….
More thinking.
T: Ten thousand?
High five!
I zip up her sweatshirt and send her out the door to catch her bus.
So What Do We Learn?
A recent research article argued that children learn a lot about place value through everyday conversation, and that kindergarteners know a lot more about the structure of the number system than parents and kindergarten teachers (on average) think they do.
Here you can see that knowledge in action. Tabitha knows that 1000 is a big and important number. She knows the pattern that allows you to keep counting by hundreds. She has not put these two pieces together. A short conversation helped her put those two pieces together, and then to extend the pattern.
Starting the conversation
This didn’t start out as a math talk. It began as a clothing inspection. But the opportunity presented itself. Listen for those times your children use numbers, and ask follow up questions about them. You won’t get this much learning out of every such conversation, but if even 10% of those opportunities turn into a little bit of learning, the interest compounds.