Counting fingers
A while back I met a mathematician. He is the husband of a colleague. He found my Talking Math with Your Kids project fascinating and asked repeatedly for additional examples of the conversations I have had with Griffin and Tabitha.
He referred to my work as brainwashing, using the term with great delight.
He shared a story of a young child who, when asked Do you have more fingers on your right hand, or on your left hand? responded without counting, but by matching the fingers thumb-to-thumb, index-to-index, et cetera.
The child invented one-to-one correspondence! my mathematician friend exclaimed with pleasure.
In a sense this is true.
There are things that we tell children. And there are ideas they have on their own, without knowing that anyone has had these ideas before. These really are inventions.
Children can invent more than we sometimes suppose they can.
In any case, this mathematician friend of mine was very curious to know what Tabitha would make of this story. I promised him I would ask. Here is what happened.
—
We were lying on the bed one evening, having just finished a book and with a few minutes left before beginning the remaining bedtime rituals.
Me: Tabitha, I want to ask you a question.
I told her that I had met a mathematician who was curious to know what she thought about something, and that this something had to do with an interesting answer that another child had once supplied to a question.
Me: The question asked of this child was, “Do you have more fingers on your left hand or on your right hand?”
Tabitha (six years old): That question doesn’t make any sense!
Me: But it’s the question that was asked.
T: But it doesn’t make any sense. Look.
[She counted the fingers first on her left hand, then on her right]
T: 1, 2, 3, 4, 5…1, 2, 3, 4, 5.
Me: So it’s the same on both hands.
T: Right, so the question doesn’t make any sense.
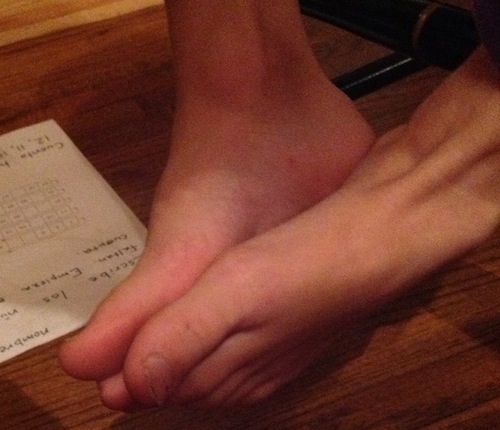
Me: OK. But that’s not how the child answered it. The child did this.
Above, you see what the child did originally.
Tabitha re-enacted it later for the purposes of this post. We regret any confusion.
Me: The question I want to ask you is, what do you think the child was thinking?
T: Oh, I know what she was thinking!
Me: Really?
T: Yeah. It’s the same. If they all touch it’s the same number.
Me: I wonder if that would work with toes.
Tabitha proceeded to demonstrate that it does in fact work with toes.
Me: Ha! I was thinking about comparing the fingers on one hand to the toes on one foot.
T: Well, it would be hard because the toes are all squished together.
We spend a few moments playing with our fingers and toes, trying to match them up, noting their relative cleanliness, and then we get on with the rest of our evening.
So what do we learn?
The technique of asking what a child thinks of an idea is a powerful one. I use it in class all the time: What do you think the person was thinking who got a different answer from you? How do you think Brianna knew to do that?
Asking children to evaluate and comment on the ideas of others helps them also to think about their own thinking.
The specific idea we discussed here is that of one-to-one correspondence. We discussed this in the recent conversation about holding hands at the farmers’ market.
Starting the conversation
This is an easy one. It doesn’t depend on your child providing an idea or knowing any particular fact of mathematics. Sometime soon, you will have a quiet moment together. Maybe it will be at the end of an all-out living room danceathon, or after reading a big pile of books. Tell your child about the mathematician’s question. Show your child the answer that so impressed the mathematician and ask, What do you think the child was thinking?
I had this same conversation with a highly precocious three-year old recently. She insisted that you needed to count the fingers in order to be sure. We had a fine time doing that. Tabitha was within earshot of the conversation with a wry smile.